Verkle Trie 从 0 到 1

video: https://youtu.be/yfQ0CUU4zik

docs: https://qiwihui.notion.site/Verkle-trie-8fa545dff5014191bfb6af2765b42e6e?pvs=4

Problems

1. How to store multiple files remotely and know that those files haven’t been changed?

2. Given a starting 𝑥, compute 𝑥↦𝑥^3+5, and repeat that 1 million times. How to prove to someone I computed this, and did so correctly - without he having to re-run the whole thing.

   Suppose our starting number is 𝑥=2.
   - x^2 = 4
   - x^3 = x^2 * x = 4 * 2 = 8
   - X^3 + 5 = 13
   So our trace is {2, 4, 8, 13, ...}
   we will produce 3,000,001 numbers in computing the circuit.
   

→ How can we verify integrity of a vector of elements?

Solution 1: Single file hashing

For single file, we can use secure hash functions:

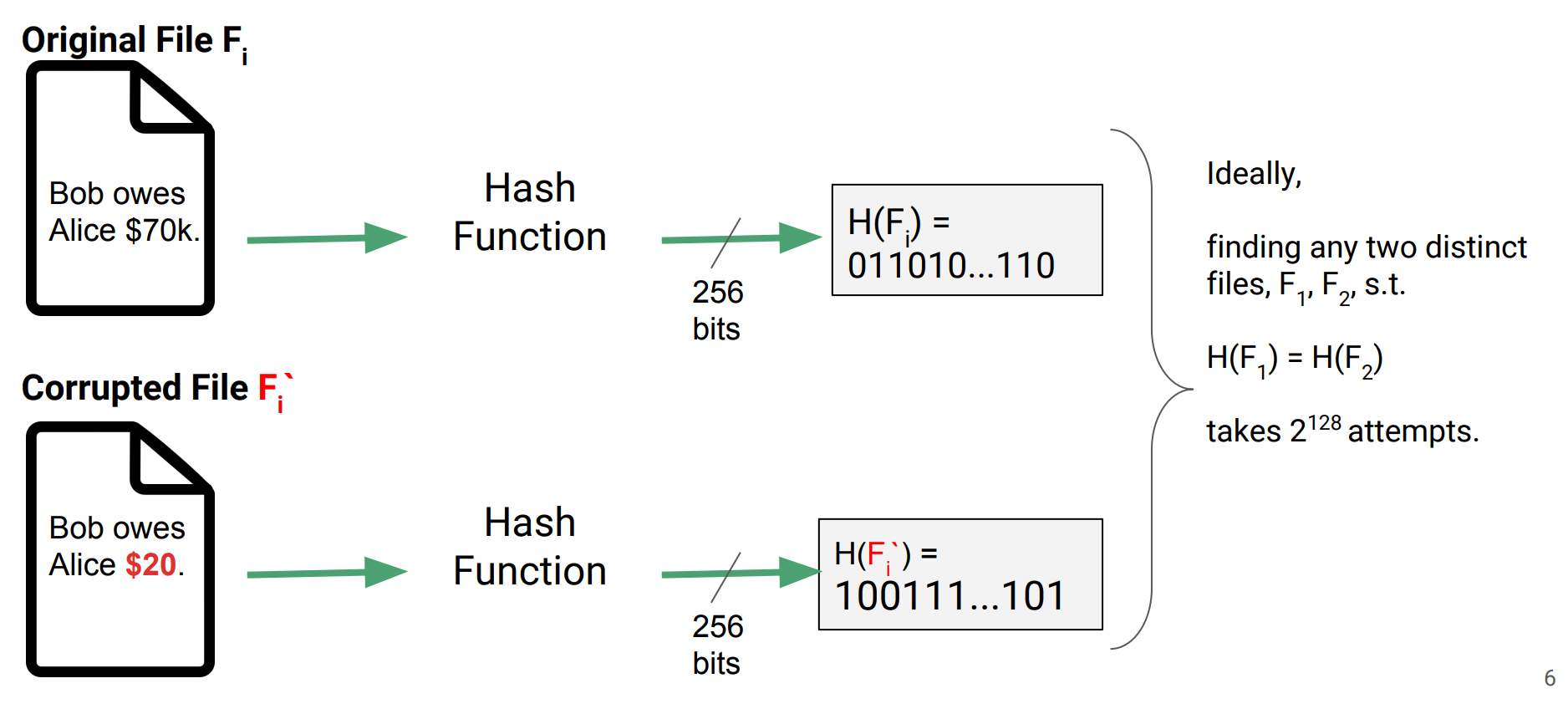
So a simple scheme for verifying file integrity: hash each file and save the store the hash locally.

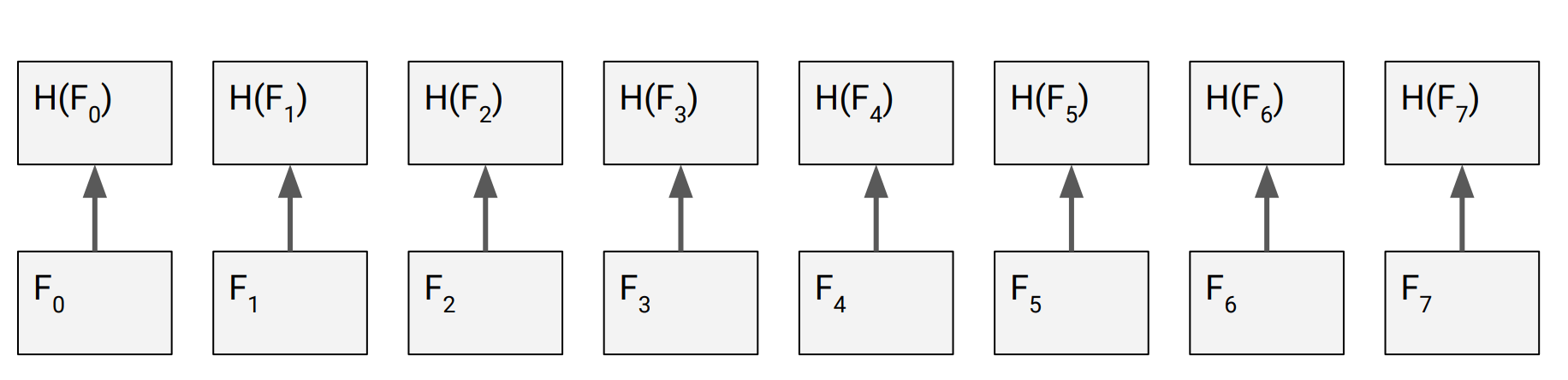
Problem: has to store n hashes → we need constant-sized digest

Solution 2: Merkle Trees

Merkle tree

• the root is the digest, it is constant sized

  

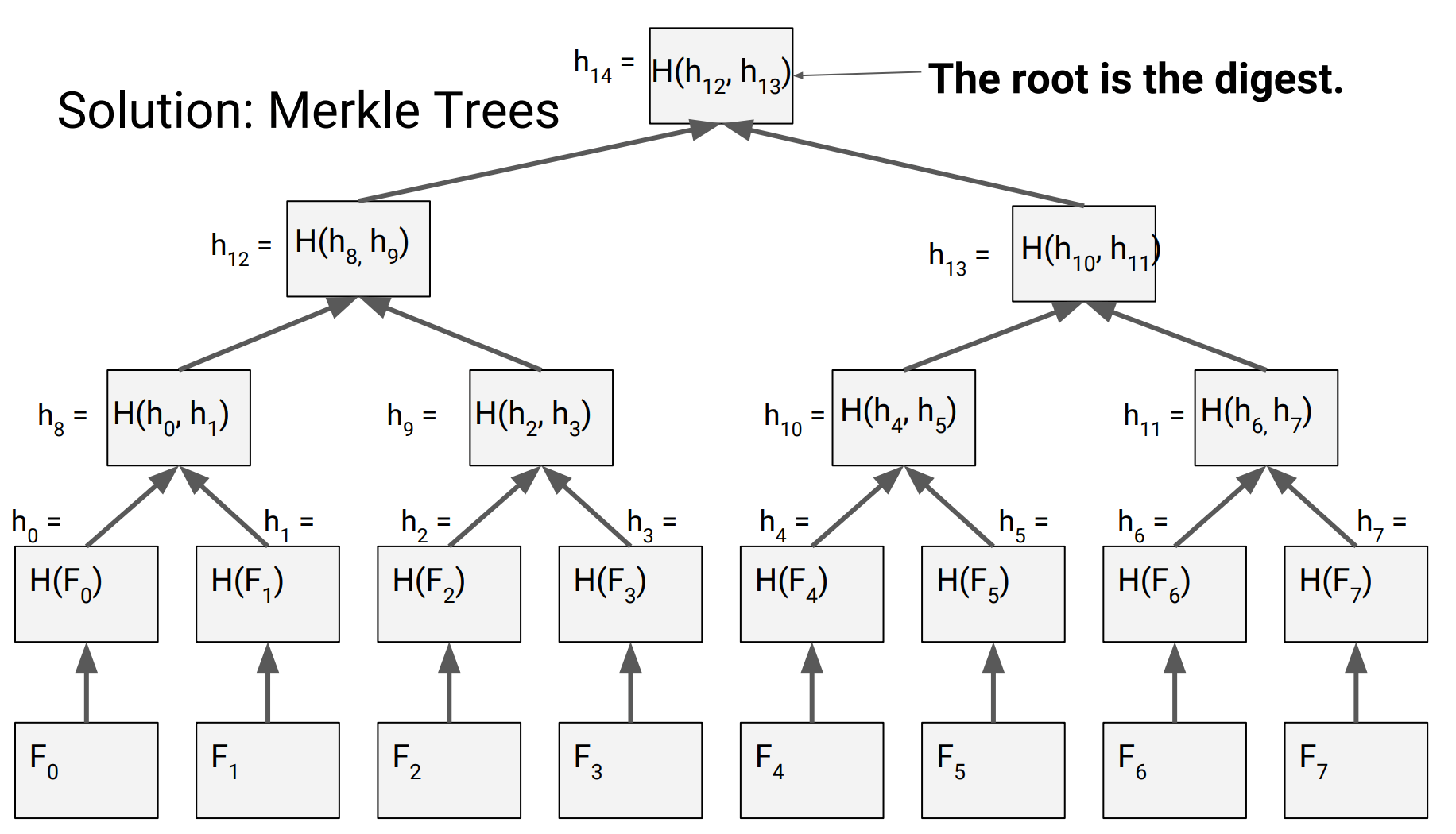
• use merkle proof to verify if the files have been changed.

  

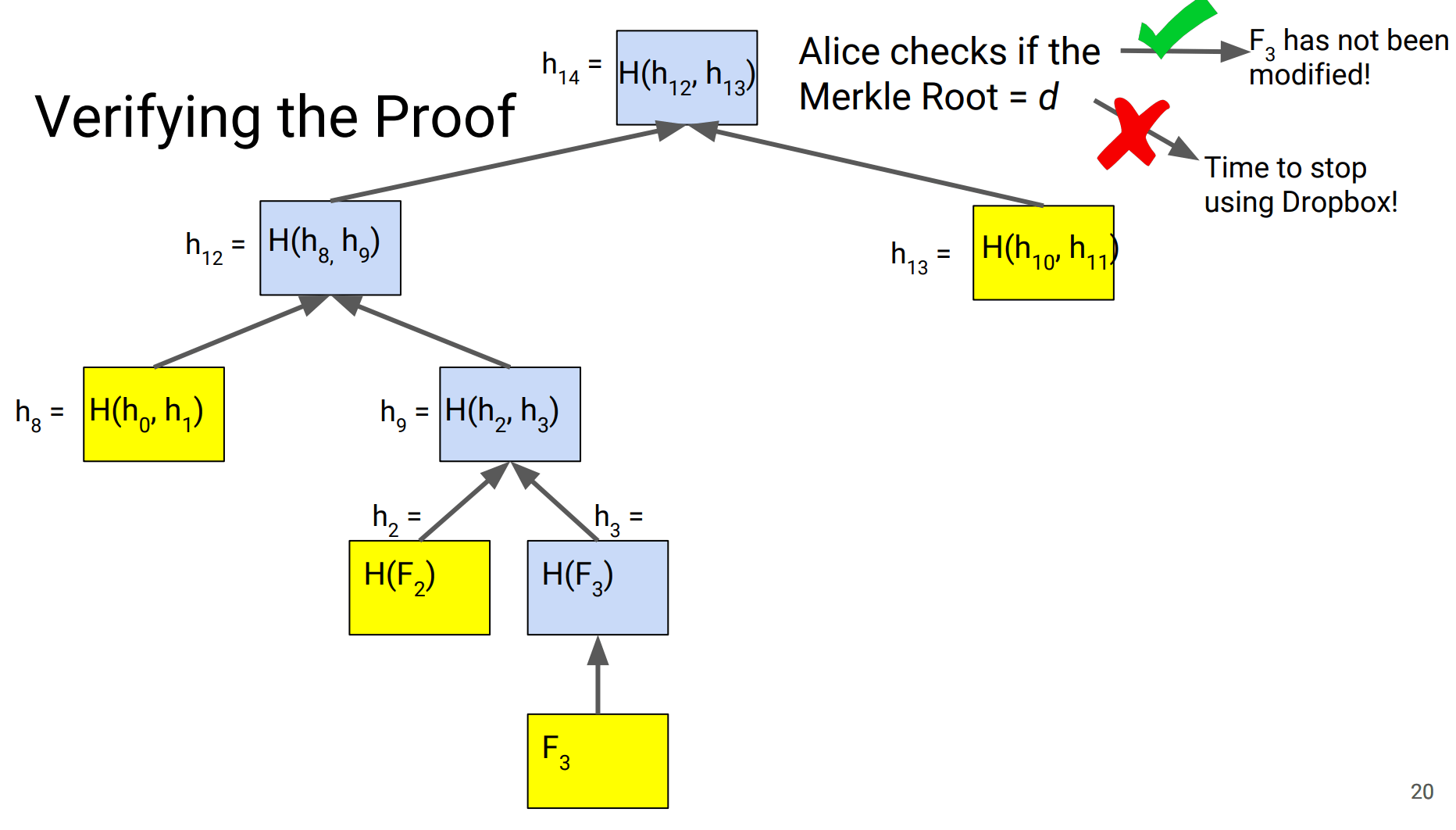
Performance

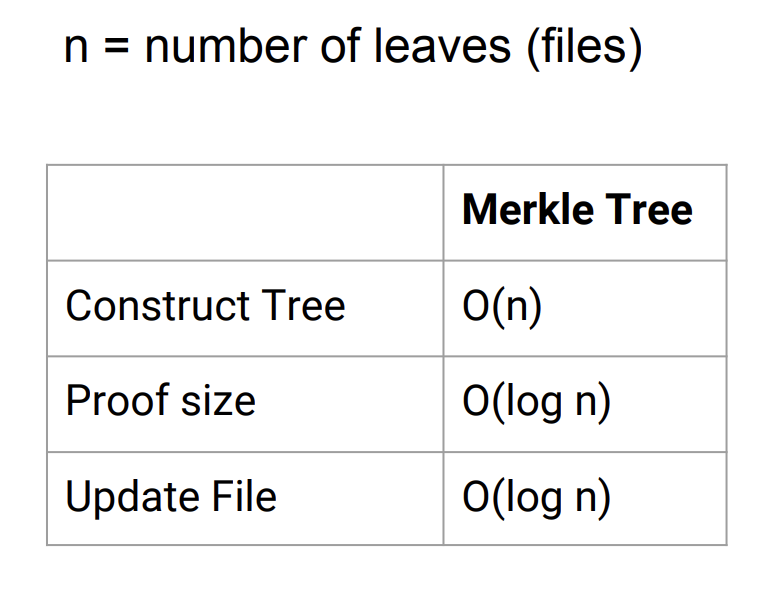
Problem: Many small files ⇒ Merkle proofs too large

Solution 3: q-ary Merkle Trees

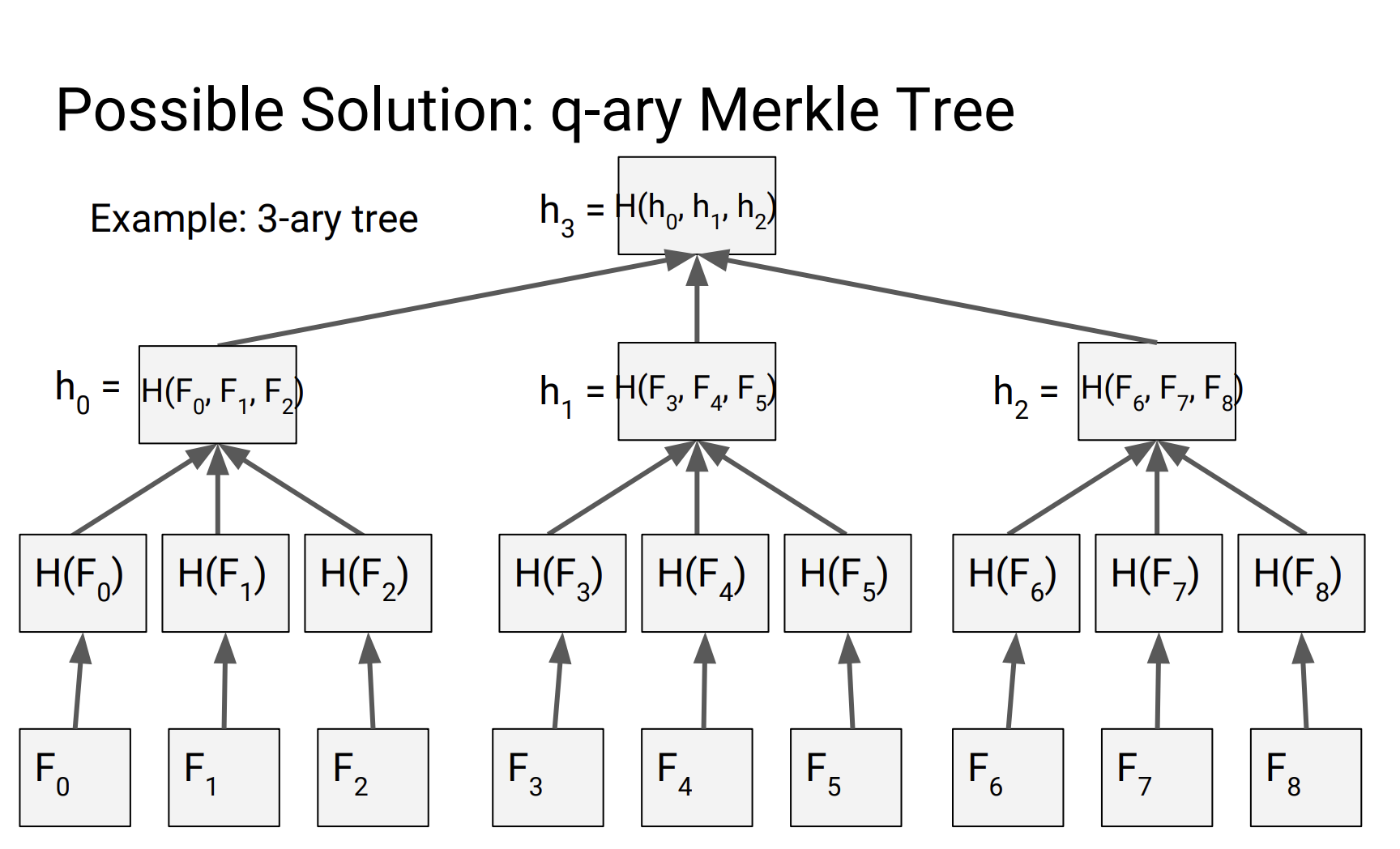
problem: Proof size is even bigger

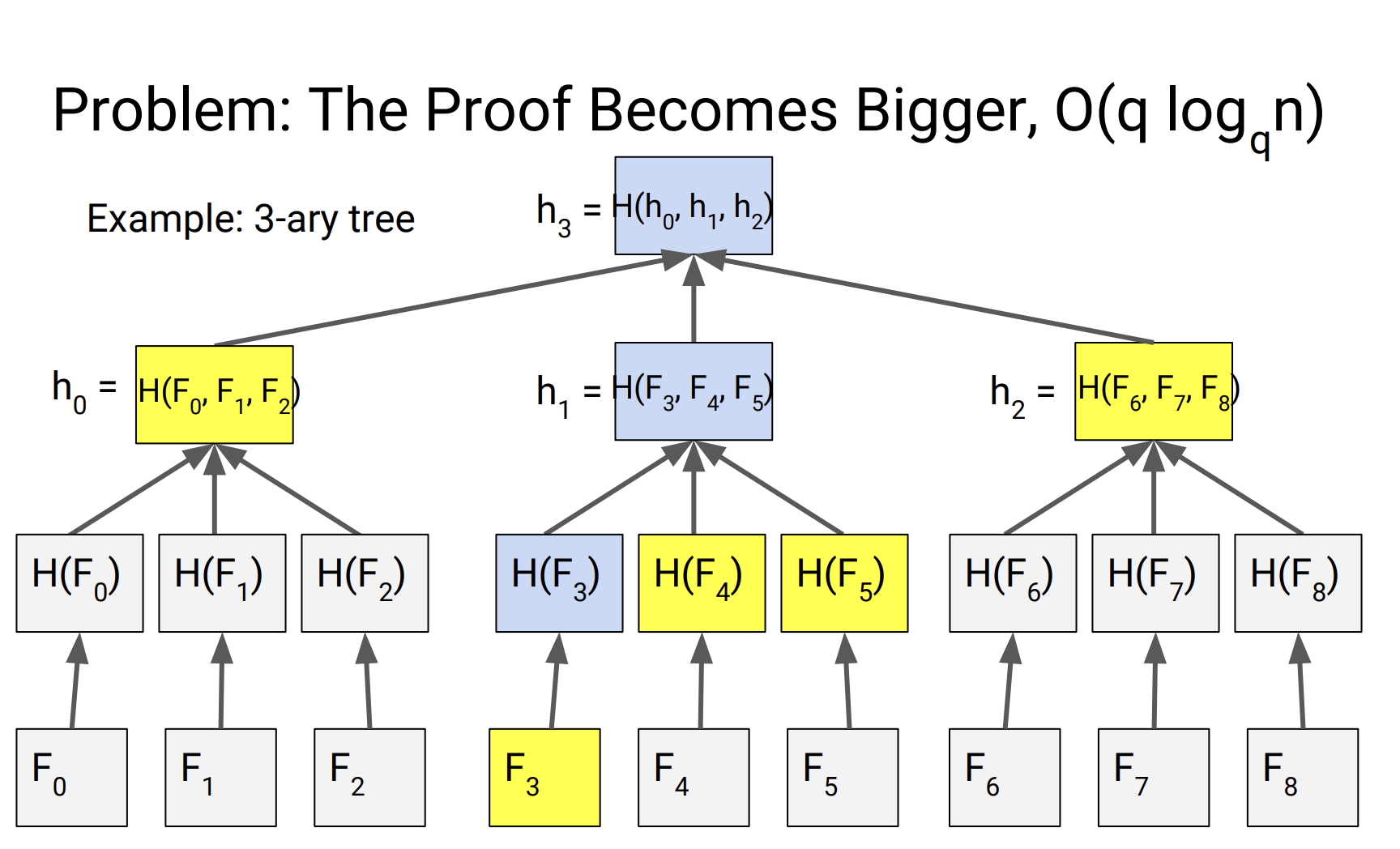
proof size: $qlo{g}_{q}n$

Solution 4: polynomial commitment

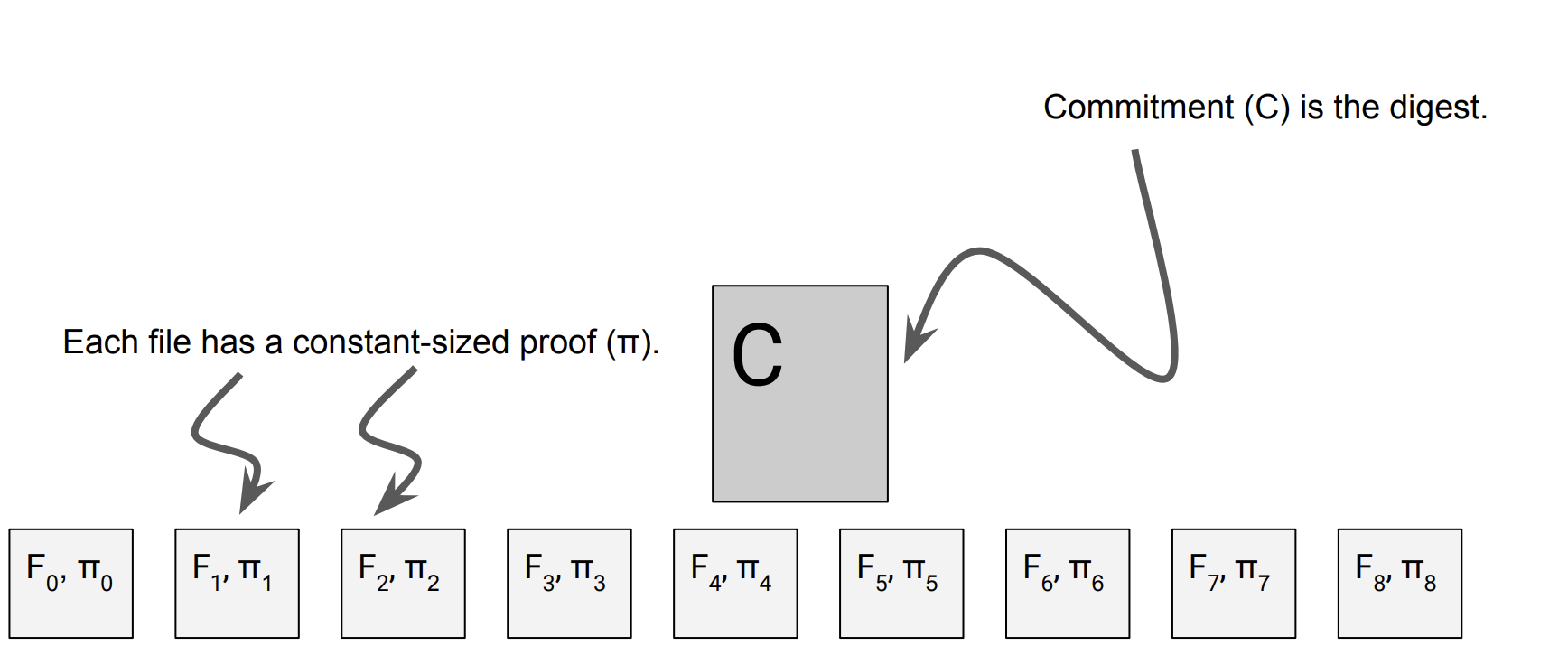
What is polynomial commitments?

1. 将长度为 $n+1$ 的 vector 转换为多项式的点值 $(v_0,v_1,\dots ,v_n)$→$(0,v_0),(1,v_1),\dots ,(n,v_n)$

2. 将唯一对应的 $Degree=n$ 的多项式$f(x)$ ，生成为Commitment→ 拉格朗日插值

   • Lagrange Interpolation

     Polynomial

     $$f(x)=\sum _{i=0}^n{a}_i{x}^i=a_0+a_{1}x+\dots +a_n{x}^n$$

     • Degree $deg(f(x))=n$
     • $a_n\ne 0$

     Encoding data into Polynomial using Lagrange Interpolation

     Given $(x_i,y_i),x_i\ne x_j,\forall i\ne j$, build a polynomial such that $f(x_i)=y_i$ and degree is $n-1$

     $$f(x)=\sum _{i=0}^{n-1}{y}_i\prod _{j=0,j\ne i}^{n-1}\frac{x-x_j}{x_i-x_j}$$

     $n=2$

     $$f(x)=y_0\frac{x-x_1}{x_0-x_1}+y_1\frac{x-x_0}{x_1-x_0}$$

     $n=3$

     $$f(x)=y_0\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}+y_1\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}\dots$$

     Example

     • Given (0, 3), (1, 6), we have

     $$f(x)=3(x-1)/(0-1)+6(x-0)/(1-0)=-3x+3+6=3x+3$$

     (2, 9), (3, 12), (4, 15). Suppose, given (1,6) and (3,12)

     $$f(x)=6(x-3)/(1-3)+12(x-1)/(3-1)=-3x+9+6x-6=3x+3$$

     n encode to m (m > n), n-of-m data can recover the polynomial exactly!

3. Open 其中的一个点，提供一个 Proof 证明点值$(k,v_k)$符合多项式$f(k)=v_k$

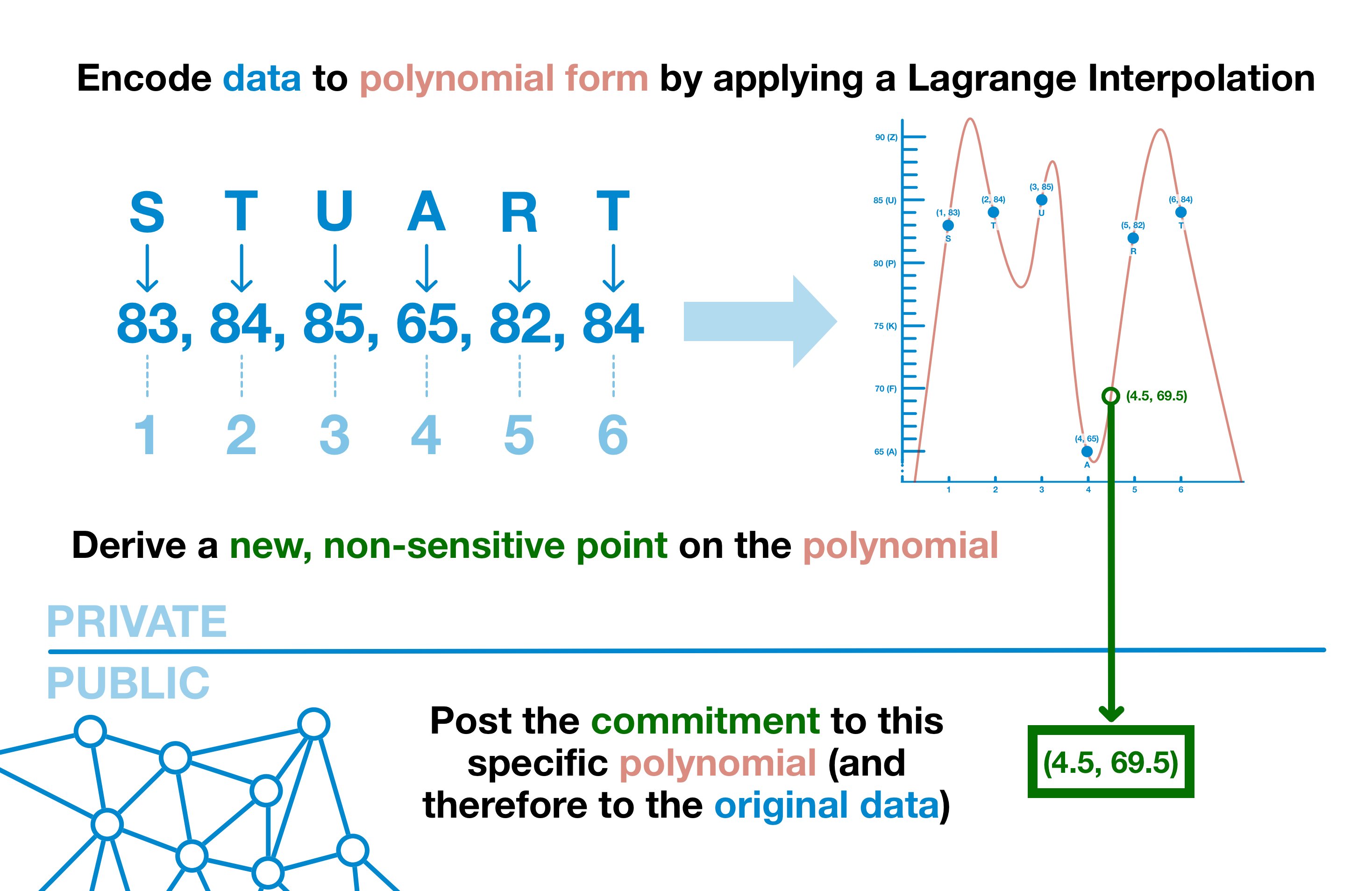
STUART → (1, 83), (2, 84), …, (6, 84) → f(x) → choose (4.5, 69.5) as commitment

KZG polynomial commitment

Knowledge -> Point-Values -> Coefficients -> Commitment -> Open&Prove&Verify
                         FFT             MSM
                                          ^
                                          |
                                    Trusted Setup

FFT: Fast Furious Transform

MSM: multi-scalar multiplication

1. KZG Commitment 是 Polynomial Commitment 的一种算法实现

   • Elliptic curves + discrete logarithm problem

     Encoding Polynomial in a finite field ${\mathbb{F}}_q$, q is prime:

     Polynomial on an elliptic curve ${\mathbb{G}}_1$

     ${\mathbb{G}}_1=[0,G_1,G_1+G_1=[2]G_1,[3]G_1,\dots ,[q]G_1]$ where $[q+1]G_1=0$

     • $[n]G_1=[n{]}_1$ can be computed very fast
     • $[n]X=Y$, given $X$ and $Y$, it is very hard to find $n$ (it is called discrete logarithm algorithm)
     • mod 7:
       • 1 mod 7, 8 mod 7, 15 mod 7,….
       • [n] mod 7 = 1 mod 7?

     $$[f(x)]G_1=[\sum _{i=0}^n{a}_i{x}^i]G_1=\sum _{i=0}^n[a_i]([x^i]G_1)=\sum _{i=0}^n[a_i][x^i{]}_1$$

   • Trusted setup

     

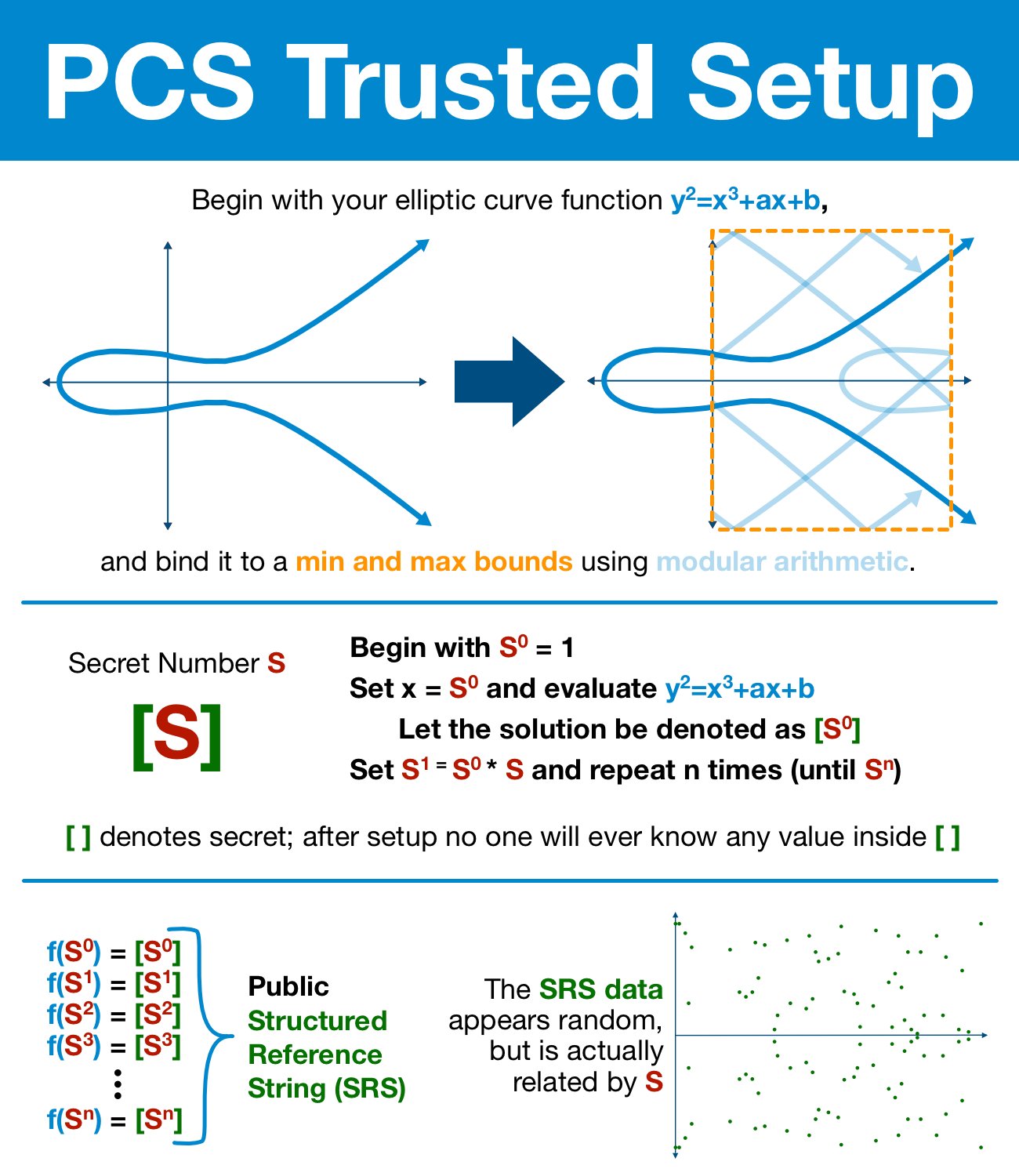
     Now we have secret $s\in {\mathbb{F}}_q$ such that

     • Nobody knows $s$ (private key of the “god”)
     • $[s^i]G_1=[s^i{]}_1$, $i=1,\dots$ is known to everybody (”god”’s public key)

     Then, we have the commitment as

     $$C=[f(s){]}_1=\sum _{i=0}^n[a_i][s^i{]}_1$$

     Finding another $g(x)$ such that $g(s)=f(s)$ is almost impossible

   • Elliptic curves pairings

     Find two elliptic curves, such that

     

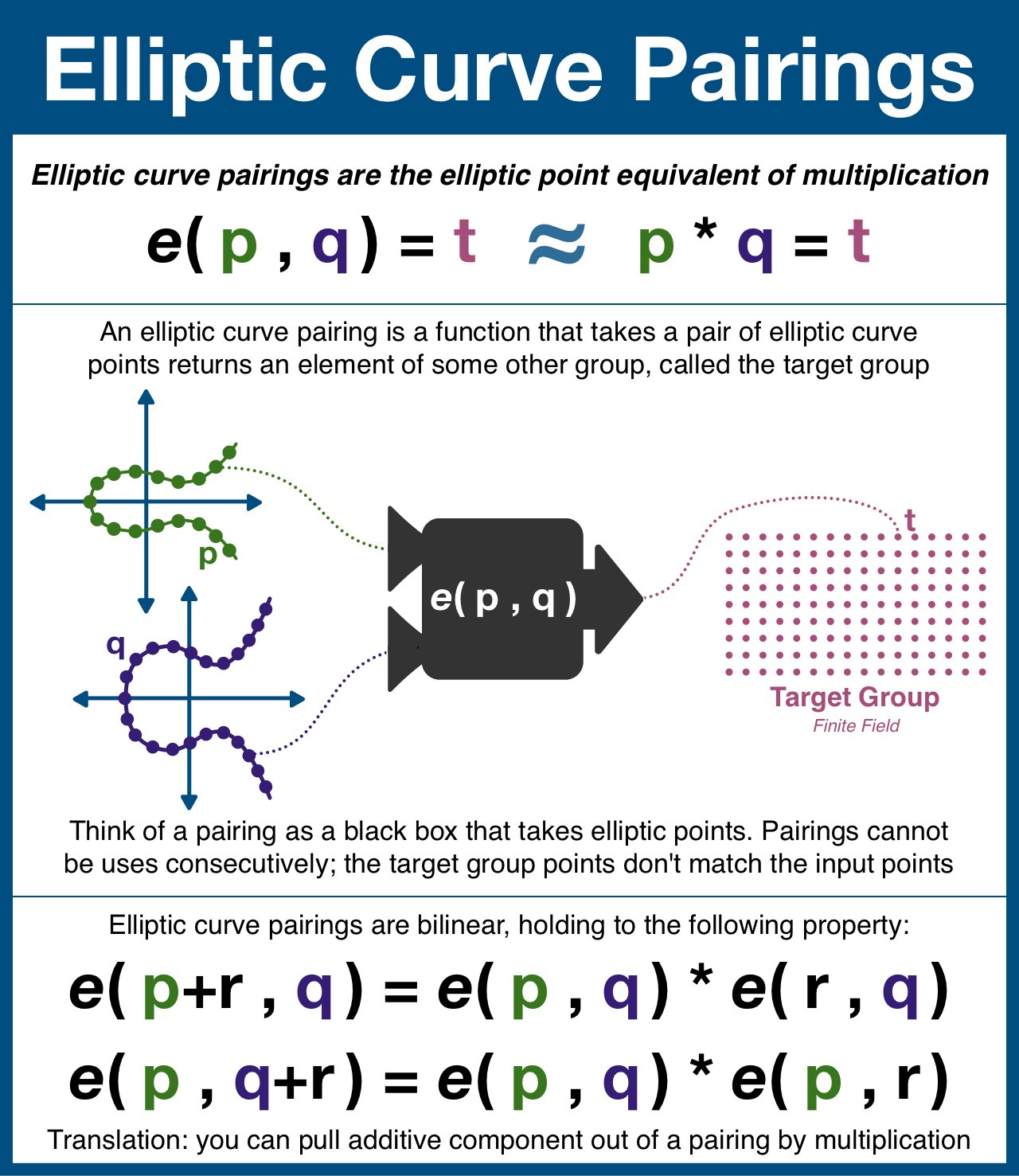
     Given $x_i,y_i$, want to prove $f(x_i)=y_i$,

     $$f(x)-y_i=g(x)=(x-x_i)q(x)$$

     3x+3 given data points( 1, 6), (4,2)

     $3x+3-6=3x-3=3(x-1)=q(x)(x-1)$

     $$\begin{array}{rl}[f(s)-y_i]G_1& =[(s-x_i)q(s)]G_1\\ C-[y_i{]}_1& \end{array}$$

     $e:{\mathbb{G}}_1\times {\mathbb{G}}_2\to {\mathbb{G}}_T$

     $$e(C-[y_i]G_1,G_2)=e([q(s){]}_1,[(s-x_i){]}_2)$$

     where $[q(s){]}_1$ is the proof (48 bytes as a point on an elliptic curve)

     

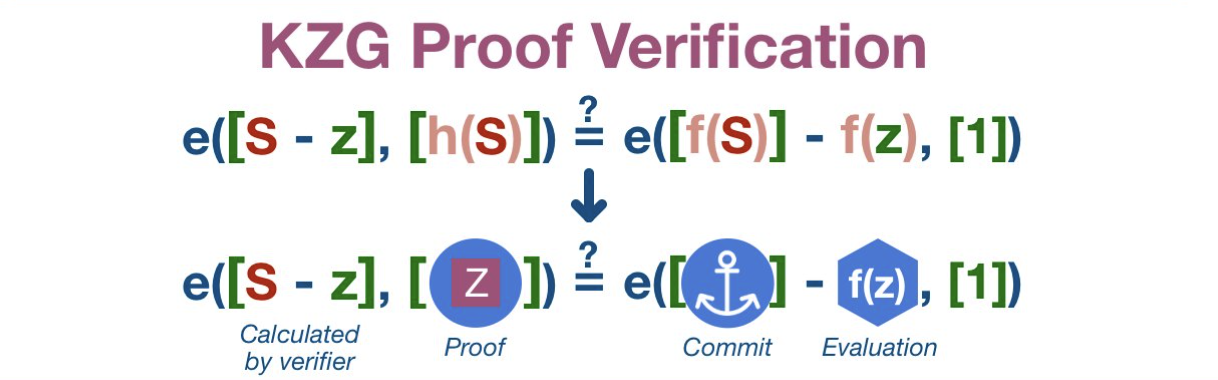
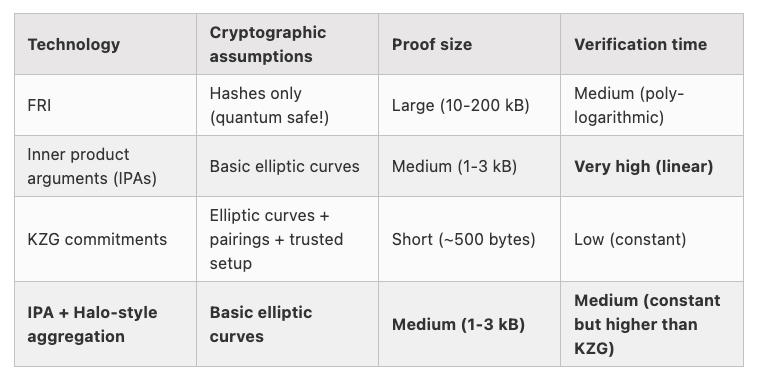
2. Polynomial Commitment 的其他实现

   1. KZG：PLONK、Marlin
   2. FRI：zkSTARK
   3. IPA：Bulletproof
   4. IPA + Halo-style aggregation：Halo 2

   

   https://vitalik.ca/general/2021/11/05/halo.html

3. KZG Commitment的优缺点

   1. 缺点：需要Trusted Setup
   2. 优点：proof 长度短且恒定

Solution 5: Verkle trie

Replace Hash Functions in q-ary Merkle tree with Vector commitment Schemes → Verkle Trie

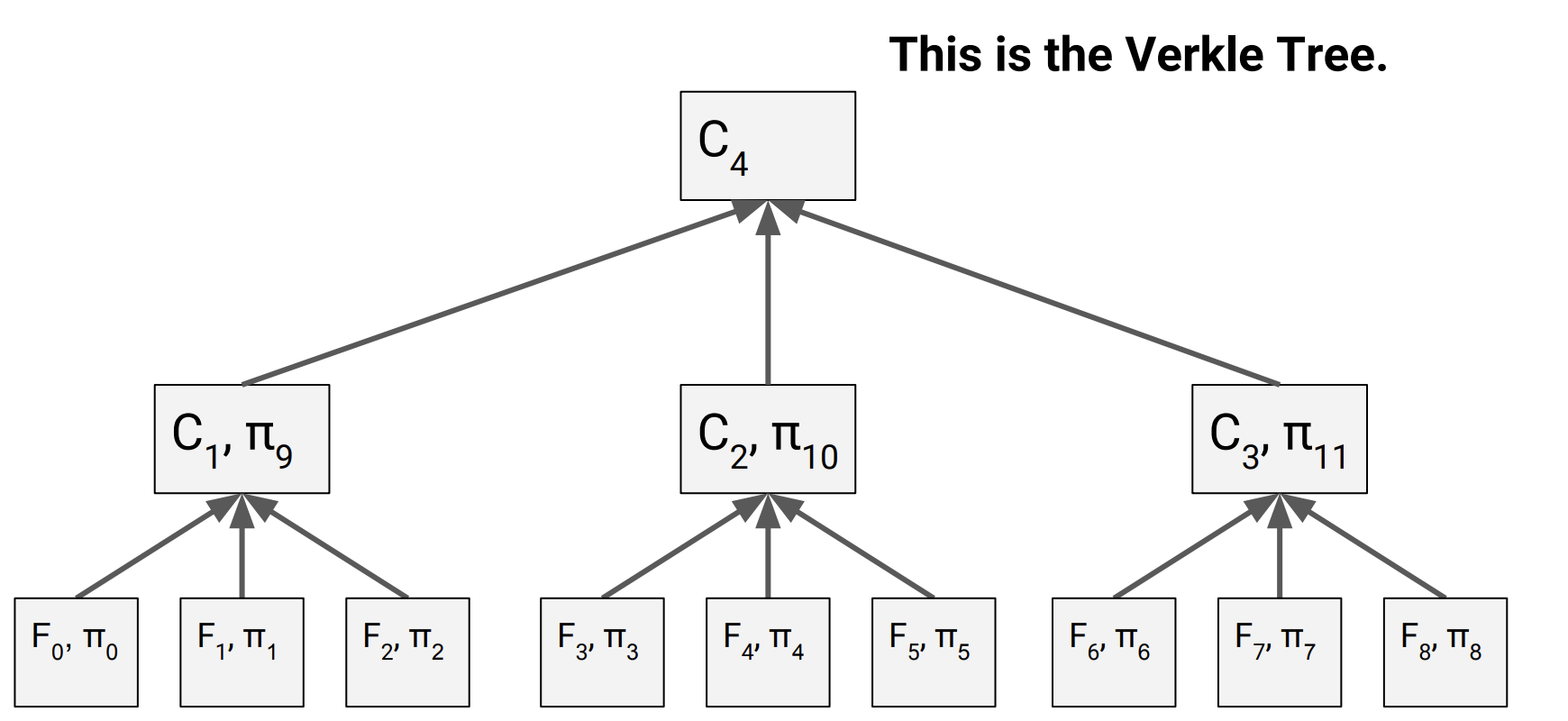
Performance comparison:

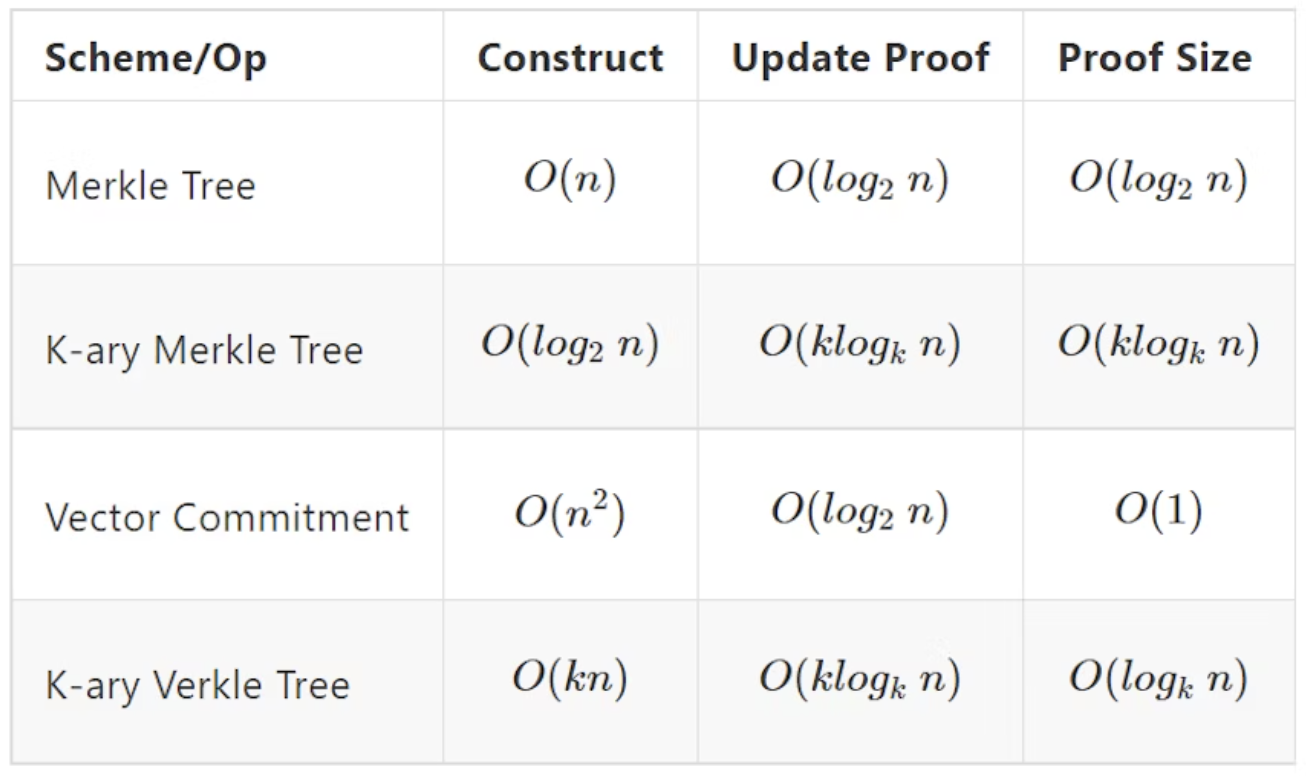
Verkle Trees let us trade off proof-size vs. construction time.

Verkle tree structure in Ethereum

MPT(Merkle Patricia Trie) problem

Ethereum has a total of four trees:

• the World State Trie
• Receipts Trie
• Transaction Trie
• Account Storage Trie

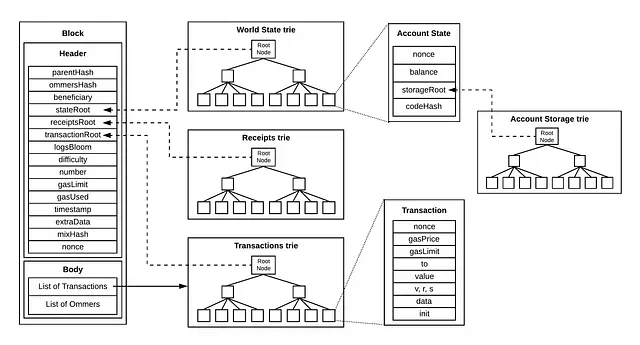
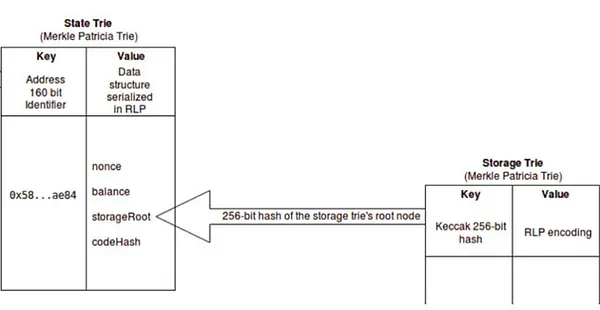
MPT is 2-layer structure (Tree-inside-a-tree)

• Complexity
• Imbalance
• Difficulty in understanding interactions between mechanisms such as state expiration

Vitalik has proposed a single-layer structure.

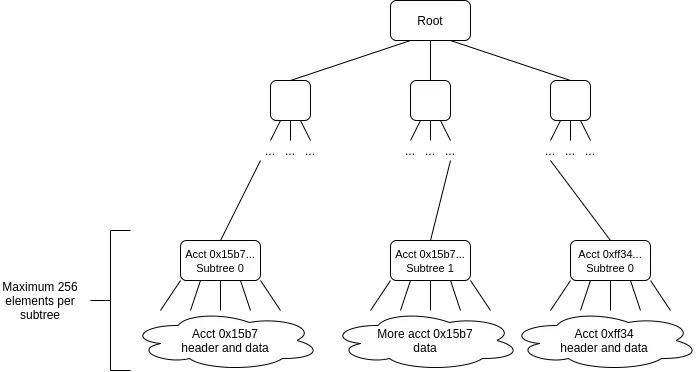
maps data to a 32-byte single key at all locations within the state:

eg. (address, storage_slot), (address, NONCE), (address, balance),…

values sharing the first 31 bytes of the key are included in the same bottom-layer commitment.

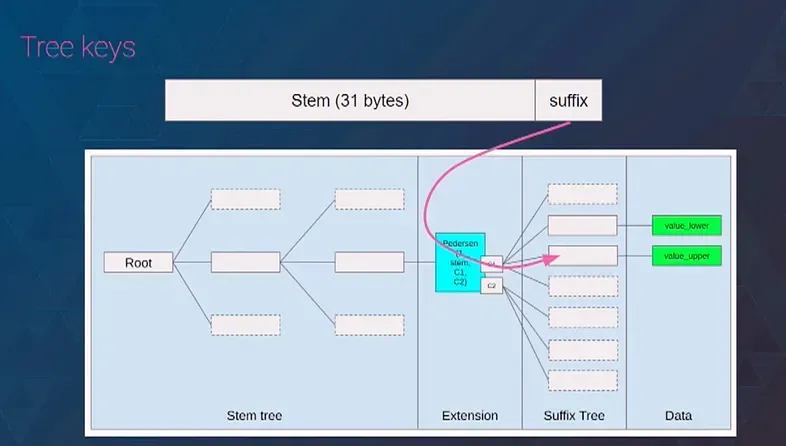
Tree key

• 32 bytes

• consisting of a 31-byte stem and a 1-byte suffix. The suffix allows for distinguishing the state information (account header data, code, storage) stored by the Tree Key.

• 31-byte stem: pedersen_hash

  def get_tree_key(address: Address32, tree_index: int, sub_index: int):
      # Asssumes VERKLE_NODE_WIDTH = 256
      return (
          pedersen_hash(address + tree_index.to_bytes(32, 'little'))[:31] +
          bytes([sub_index])
      )
  

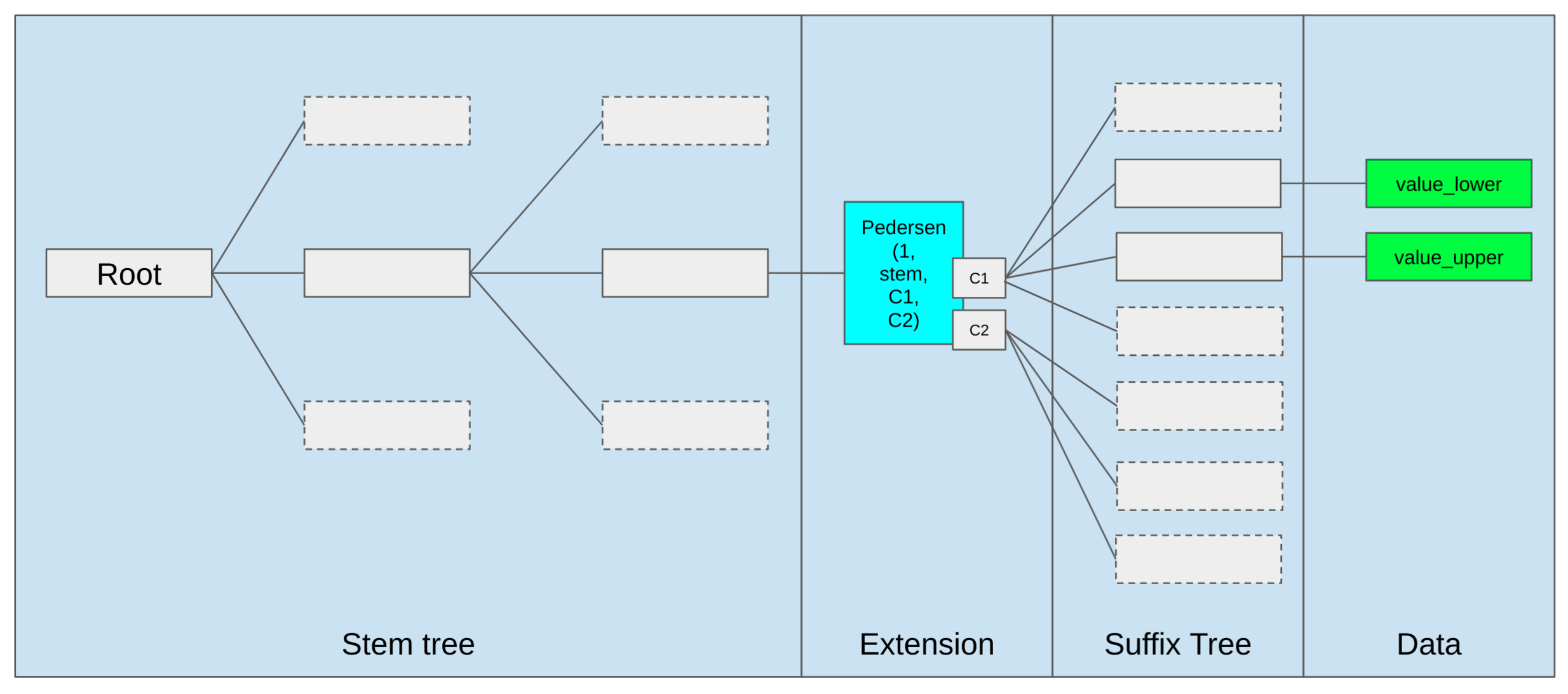
verkle tree structure:

Inner Node & Suffix Node(extension node)

Suffix Node

suffix node structure:

• 1: A marker for the suffix node, which is 1 on the elliptic curve but does not literally mean the number 1.
• Stem: The stem refers to the stem in the tree key.
• C1, C2: Are Pedersen Commitments.

C = Commit(1, C1, Stem, C2)

C1 and C2 commitment take the data form:

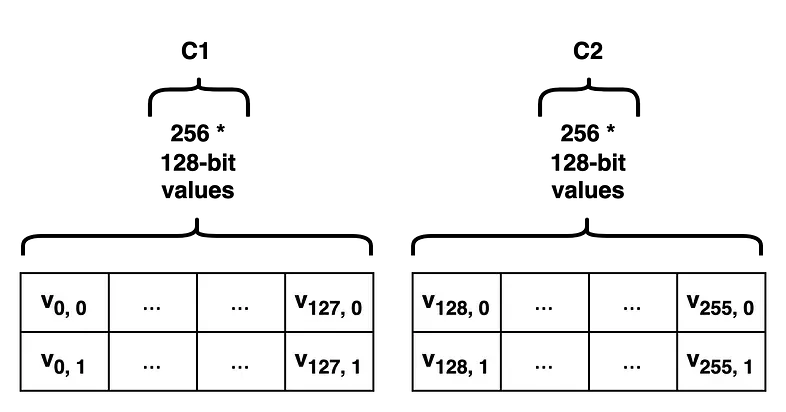
• The reason for this division is that the creation of Pedersen Commitment is limited to committing up to 256 values of maximum 253-bit size, and for 256-bit values, data loss occurs.
• Process of storing 32-byte data under a tree key:

  1. Depending on the suffix, the data become v0, v1… v255

  2. v0~v127 are included in C1, and v128~v255 are included in C2 to calculate the leaf node’s commitment

  3. For C1, each 32-byte value of v0~v127 is divided into the upper 16 bytes (v1,0) and the lower 16 bytes (v1, 1) to serve as coefficients in a polynomial.

     → each coefficient’s data being 16 bytes (128-bit)

  4. 256-degree polynomial is committed:

     • C1 = commit([(v0,0), (v0,1), (v1,0), (v1,1)…(v127,0),(v127,1)])
     • C2 = commit([(v128,0), (v128,1), (v129,0), (v129,1) … (v255,0),(v255,1)])

  5. C = Commit(1, C1, Stem, C2) → commitment for the leaf node

Inner Node

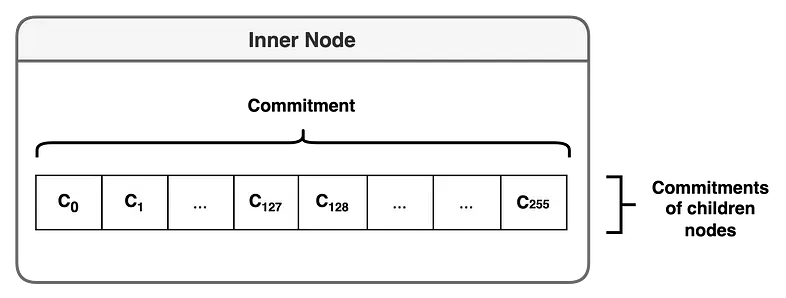
• holds the stem value of the tree key and stores 256 pointers to sub-nodes
• C0, C1 … C255 represent the commitments of sub-nodes, and the inner node contains these commitments.

An example of verkle tree containing 4 tree keys:

• 0x00..20
• 0xdefe…64
• 0xde03a8..02
• 0xde03a8..ff

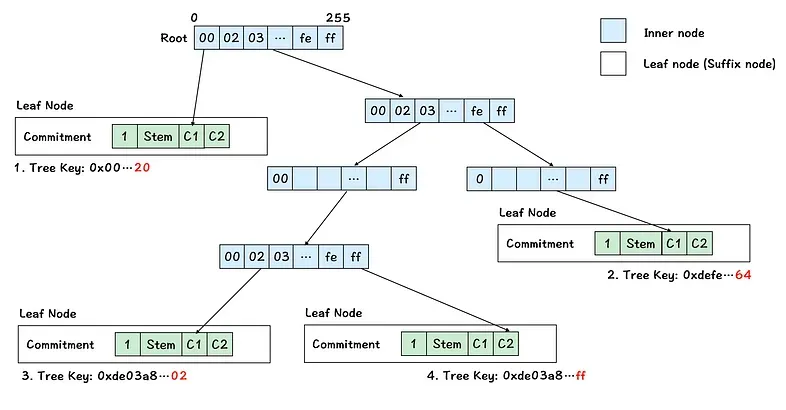
Summary:

• The Verkle Trie consists of two types of nodes: leaf nodes and inner nodes.
• A tree key contains a stem and a suffix.
• The same stem corresponds to the same leaf node.
• Data is stored differentiated by the suffix of the tree key.
• The tree key is encoded byte by byte along the path from the root to the leaf node.
• Data is included in the commitment of the leaf node.